number system

	Numbering System
		Many number systems are in use in digital technology. The most common are the decimal, binary, octal, and hexadecimal systems. The decimal system is clearly the most familiar to us because it is a tool that we use every day. Examining some of its characteristics will help us to better understand the other systems. In the next few pages we shall introduce four numerical representation systems that are used in the digital system. There are other systems, which we will look at briefly.
		Decimal Binary Octal Hexadecimal
		Decimal System
		The decimal system is composed of 10 numerals or symbols. These 10 symbols are 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Using these symbols as digits of a number, we can express any quantity. The decimal system is also called the base-10 system because it has 10 digits.
		103 102 101 100 10-1 10-2 10-3 =1000 =100 =10 =1 . =0.1 =0.01 =0.001 Most Significant Digit Decimal point Least Significant Digit
		Even though the decimal system has only 10 symbols, any number of any magnitude can be expressed by using our system of positional weighting.
		Decimal Examples
		3.1410 5210 102410 6400010
		Binary System
		In the binary system, there are only two symbols or possible digit values, 0 and 1. This base-2 system can be used to represent any quantity that can be represented in decimal or other base system.
		23 22 21 20 2-1 2-2 2-3 =8 =4 =2 =1 . =0.5 =0.25 =0.125 Most Significant Digit Binary point Least Significant Digit
		Binary Counting
		The Binary counting sequence is shown in the table:
		23 22 21 20 Decimal 0 0 0 0 0 0 0 0 1 1 0 0 1 0 2 0 0 1 1 3 0 1 0 0 4 0 1 0 1 5 0 1 1 0 6 0 1 1 1 7 1 0 0 0 8 1 0 0 1 9 1 0 1 0 10 1 0 1 1 11 1 1 0 0 12 1 1 0 1 13 1 1 1 0 14 1 1 1 1 15
		Representing Binary Quantities
		In digital systems the information that is being processed is usually presented in binary form. Binary quantities can be represented by any device that has only two operating states or possible conditions. E.g.. a switch is only open or closed. We arbitrarily (as we define them) let an open switch represent binary 0 and a closed switch represent binary 1. Thus we can represent any binary number by using series of switches.
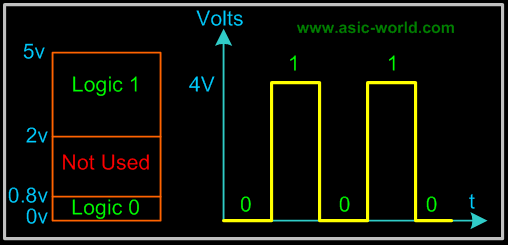
		Typical Voltage Assignment
		Binary 1: Any voltage between 2V to 5V
		Binary 0: Any voltage between 0V to 0.8V
		Not used: Voltage between 0.8V to 2V in 5 Volt CMOS and TTL Logic, this may cause error in a digital circuit. Today's digital circuits works at 1.8 volts, so this statement may not hold true for all logic circuits.
		We can see another significant difference between digital and analog systems. In digital systems, the exact voltage value is not important; eg, a voltage of 3.6V means the same as a voltage of 4.3V. In analog systems, the exact voltage value is important.
		The binary number system is the most important one in digital systems, but several others are also important. The decimal system is important because it is universally used to represent quantities outside a digital system. This means that there will be situations where decimal values have to be converted to binary values before they are entered into the digital system.
		In additional to binary and decimal, two other number systems find wide-spread applications in digital systems. The octal (base-8) and hexadecimal (base-16) number systems are both used for the same purpose- to provide an efficient means for representing large binary system.
		Octal System
		The octal number system has a base of eight, meaning that it has eight possible digits: 0,1,2,3,4,5,6,7.
		83 82 81 80 8-1 8-2 8-3 =512 =64 =8 =1 . =1/8 =1/64 =1/512 Most Significant Digit Octal point Least Significant Digit
		Octal to Decimal Conversion
		2378 = 2 x (82) + 3 x (81) + 7 x (80) = 15910 24.68 = 2 x (81) + 4 x (80) + 6 x (8-1) = 20.7510 11.18 = 1 x (81) + 1 x (80) + 1 x (8-1) = 9.12510 12.38 = 1 x (81) + 2 x (80) + 3 x (8-1) = 10.37510
		Hexadecimal System
		The hexadecimal system uses base 16. Thus, it has 16 possible digit symbols. It uses the digits 0 through 9 plus the letters A, B, C, D, E, and F as the 16 digit symbols.
		163 162 161 160 16-1 16-2 16-3 =4096 =256 =16 =1 . =1/16 =1/256 =1/4096 Most Significant Digit Hexa Decimal point Least Significant Digit
		Hexadecimal to Decimal Conversion
	Code Conversion Converting from one code form to another code form is called code conversion, like converting from binary to decimal or converting from hexadecimal to decimal.       Binary-To-Decimal Conversion Any binary number can be converted to its decimal equivalent simply by summing together the weights of the various positions in the binary number which contain a 1.     Binary Decimal 110112 24+23+01+21+20 =16+8+0+2+1 Result 2710     and     Binary Decimal 101101012 27+06+25+24+03+22+01+20 =128+0+32+16+0+4+0+1 Result 18110     You should have noticed that the method is to find the weights (i.e., powers of 2) for each bit position that contains a 1, and then to add them up.       Decimal-To-Binary Conversion     There are 2 methods:     Reverse of Binary-To-Decimal Method Repeat Division       Reverse of Binary-To-Decimal Method     Decimal Binary 4510 =32 + 0 + 8 + 4 +0 + 1 =25+0+23+22+0+20 Result =1011012           Repeat Division-Convert decimal to binary This method uses repeated division by 2.     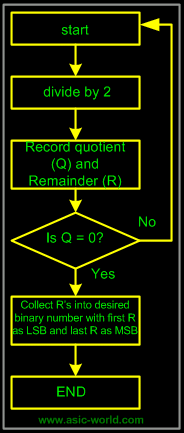Convert 2510 to binary     Division Remainder Binary 25/2 = 12+ remainder of 1 1 (Least Significant Bit) 12/2 = 6 + remainder of 0 0 6/2 = 3 + remainder of 0 0 3/2 = 1 + remainder of 1 1 1/2 = 0 + remainder of 1 1 (Most Significant Bit) Result 2510 = 110012     The Flow chart for repeated-division method is as follows:               Binary-To-Octal / Octal-To-Binary Conversion     Octal Digit 0 1 2 3 4 5 6 7 Binary Equivalent 000 001 010 011 100 101 110 111     Each Octal digit is represented by three binary digits.     Example: 100 111 0102 = (100) (111) (010)2 = 4 7 28       Repeat Division-Convert decimal to octal     This method uses repeated division by 8.     Example: Convert 17710 to octal and binary     Division Result Binary 177/8 = 22+ remainder of 1 1 (Least Significant Bit) 22/ 8 = 2 + remainder of 6 6 2 / 8 = 0 + remainder of 2 2 (Most Significant Bit) Result 17710 = 2618 Binary = 0101100012       Hexadecimal to Decimal/Decimal to Hexadecimal Conversion     Example: 2AF16 = 2 x (162) + 10 x (161) + 15 x (160) = 68710       Repeat Division- Convert decimal to hexadecimal This method uses repeated division by 16.     Example: convert 37810 to hexadecimal and binary:     Division Result Hexadecimal 378/16 = 23+ remainder of 10 A (Least Significant Bit)23 23/16 = 1 + remainder of 7 7 1/16 = 0 + remainder of 1 1 (Most Significant Bit) Result 37810 = 17A16 Binary = 0001 0111 10102       Binary-To-Hexadecimal /Hexadecimal-To-Binary Conversion     Hexadecimal Digit 0 1 2 3 4 5 6 7 Binary Equivalent 0000 0001 0010 0011 0100 0101 0110 0111     Hexadecimal Digit 8 9 A B C D E F Binary Equivalent 1000 1001 1010 1011 1100 1101 1110 1111     Each Hexadecimal digit is represented by four bits of binary digit.     Example:     1011 0010 11112 = (1011) (0010) (1111)2 = B 2 F16       Octal-To-Hexadecimal Hexadecimal-To-Octal Conversion     Convert Octal (Hexadecimal) to Binary first. Regroup the binary number by three bits per group starting from LSB if Octal is required. Regroup the binary number by four bits per group starting from LSB if Hexadecimal is required.     Example:     Convert 5A816 to Octal.     Hexadecimal Binary/Octal 5A816 = 0101 1010 1000 (Binary) = 010 110 101 000 (Binary) Result = 2 6 5 0 (Octal)	24.616 = 2 x (161) + 4 x (160) + 6 x (16-1) = 36.37510 11.116 = 1 x (161) + 1 x (160) + 1 x (16-1) = 17.062510 12.316 = 1 x (161) + 2 x (160) + 3 x (16-1) = 18.187510