k map 3

		4-Variable K-Map
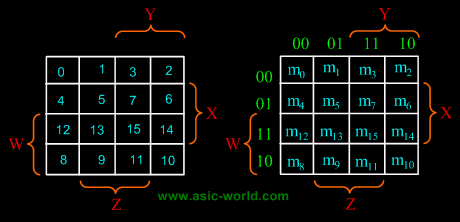
		There are 16 cells in a 4-variable (W, X, Y, Z); K-map as shown in the figure below.
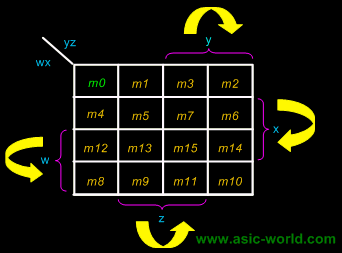
		There are 2 wrap-around: a horizontal wrap-around and a vertical wrap-around. Every cell thus has 4 neighbours. For example, the cell corresponding to minterm m0 has neighbours m1, m2, m4 and m8.
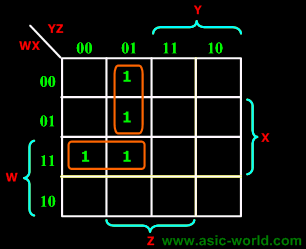
		Example
		F(W,X,Y,Z) = (1,5,12,13)
		F = WY'Z + W'Y'Z
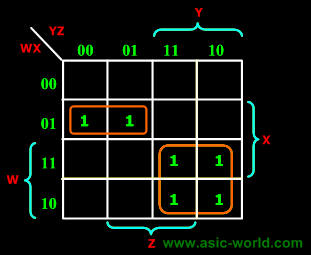
		Example
		F(W,X,Y,Z) = (4, 5, 10, 11, 14, 15)
		F = W'XY' + WY
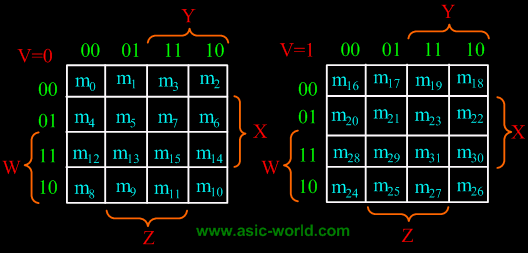
		5-Variable K-Map
		There are 32 cells in a 5-variable (V, W, X, Y, Z); K-map as shown in the figure below.
		Inverse Function
		The 0's on a K-map indicate when the function is 0. We can minimize the inverse function by grouping the 0's (and any suitable don't cares) instead of the 1's. This technique leads to an expression which is not logically equivalent to that obtained by grouping the 1's (i.e., the inverse of X != X'). Minimizing for the inverse function may be particularly advantageous if there are many more 0's than 1's on the map. We can also apply De Morgan's theorem to obtain a product-of-sum expression.