logic gates

	Logic Circuits
		Boolean algebra is ideal for expressing the behavior of logic circuits.
		A circuit can be expressed as a logic design and implemented as a collection of individual connected logic gates.
		Fixed Logic Systems
		A fixed logic system has two possible choices for representing true and false.
		Positive Logic
		In a positive logic system, a high voltage is used to represent logical true (1), and a low voltage for a logical false (0).
		Negative Logic
		In a negative logic system, a low voltage is used to represent logical true (1), and a high voltage for a logical false (0).
		In positive logic circuits it is normal to use +5V for true and 0V for false.
		Switching Circuits
		The abstract logic described previously can be implemented as an actual circuit. Switches are left open for logic 0 and closed for logic 1.
		Two variable AND circuit X.Y
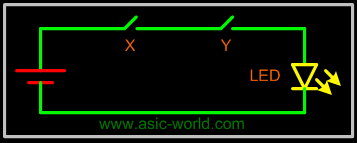		Two variable OR circuit X + Y
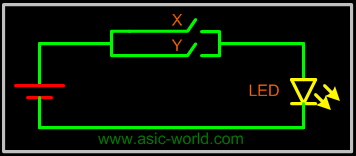		Four variable circuit U.V.(X + Y)
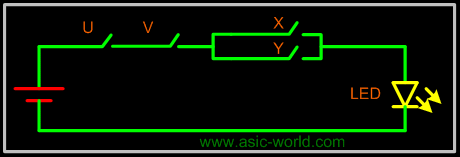		Truth Table
		A truth table is a means for describing how a logic circuit's output depends on the logic levels present at the circuit's inputs.
		In the following twos-inputs logic circuit, the table lists all possible combinations of logic levels present at inputs X and Y along with the corresponding output level F.
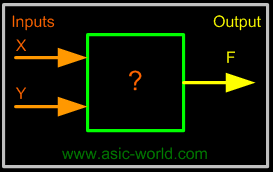		X Y F = X*Y 0 0 0 0 1 0 1 0 0 1 1 1
		When either input X AND Y is 1, the output F is 1. Therefore the "?" in the box is an AND gate.