number system 5

	Floating Point Numbers
		A real number or floating point number is a number which has both an integer and a fractional part. Examples for real real decimal numbers are 123.45, 0.1234, -0.12345, etc. Examples for real binary numbers are 1100.1100, 0.1001, -1.001, etc. In general, floating point numbers are expressed in exponential notation.
		For example the decimal number
		30000.0 can be written as 3 x 104. 312.45 can be written as 3.1245 x 102.
		Similarly, the binary number 1010.001 can be written as 1.010001 x 103.
		The general form of a number N can be expressed as
		N = ± m x b±e.
		Where m is mantissa, b is the base of number system and e is the exponent. A floating point number is represented by two parts. The number first part, called mantissa, is a signed fixed point number and the second part, called exponent, specifies the decimal or binary position.
		Binary Representation of Floating Point Numbers
		A floating point binary number is also represented as in the case of decimal numbers. It means that mantissa and exponent are expressed using signed magnitude notation in which one bit is reserved for sign bit.
		Consider a 16-bit word used to store the floating point numbers; assume that 9 bits are reserved for mantissa and 7 bits for exponent and also assume that the mantissa part is represented in fraction system. This implies the assumed binary point is at the mantissa sign bit immediate right.
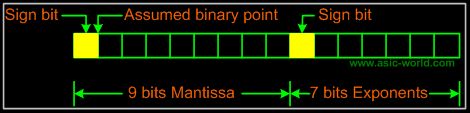		Example
		A binary number 1101.01 is represented as
		Mantissa = 110101 = (1101.01)2 = 0.110101 X 24
		Exponent = (4)10
		Expanding mantissa to 8 bits we get 11010100
		Binary representation of exponent (4)10 = 000100
		The required representation is